I know I mentioned this in class, but I'll say it again: Geometry has too many dang words. How am I, much less my students, supposed to remember all the terms?
isoceles. scalene. rhombus. humanoid*. polygon.
* just making sure you're paying attention
I'll look up lots of games and tips and tricks as my career progresses, I'm sure. But meanwhile, I need to make sure I have a rock-solid understanding of the terms themselves--beginning with that basic geometric shape: the triangle.
 |
| You will NOT break me. |
Let's start with the angles themselves.
A right angle is an angle at 90 degrees. We mark it with a little square, like this:
That's intuitive to me. I don't even need to think about it. So that's one down.Next:
An acute angle is less than 90 degrees . . .
. . . and an obtuse angle is greater than 90 degrees (but less than 180 degrees--duh, since 180 degrees would be a a straight line):
Again, these terms make intuitive sense to me:
- Acute sounds like a sharp word: "Acute!"And skinny angles look sharper to me. Plus, we use the word acute to mean "sharp," as in "acute pain."
- Obtuse sounds like a big, slow word: "Obtuuuuuse." And obtuse angles are big. Plus, we use the word obtuse to mean "blunted," or the opposite of sharp, as in, "because he hadn't read the piece, his analysis was somewhat obtuse."
So what's the problem, then? Looks like I have these terms down, amiright? Well, hold the phone:
Are you confused yet? I am.
I know an acute triangle has all acute angles and that an obtuse triangle has one obtuse angle. Just by looking at these five triangles, the only one that's obvious to me is E: It's an obtuse triangle because the bottom left angle clearly measures greater than 90 degrees:
 |
| E |
 |
| A |
Triangle A is a good segue into what confuses me the most about angles/triangles, though: Which way do we measure them?
 |
| What on earth are you talking about, Miss B? |
I'll show you what I mean. Here's triangle A again--but now I've rotated it:
 |
| A |
Let's look at this lower left angle. Clearly it's acute, right? Because we see what 90 degrees looks like, and this angle is less than 90 degrees.
But what about this lower right angle?
 |
| A |
Again, we see what 90 degrees looks like. But the y axis of the lower right angle seems like it would create an angle greater than 90 degrees to me, because it's to the left of the 90-degree y axis. And yet, the angle doesn't look obtuse. Clearly I'm missing something.
 |
| A little obtuse, are we? |
I only see one difference between the lower left angle and the lower right angle: the direction of the x axis. The lower left angle has the x axis going to the right . . .
 |
| A |
. . . and the lower right angle has the x axis going to the left:
 |
| A |
So what if the correct way to measure an angle is to rotate it until the x axis is going to the right? Let me practice a little with my good friends at--say it with me--Khan Academy, and see if my theory holds up.
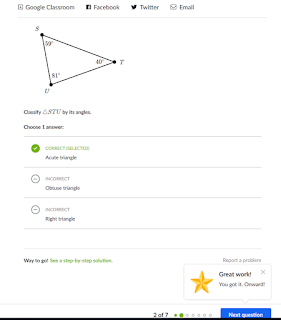
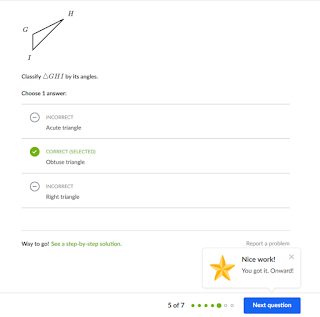
Here's a practice set for identifying triangles by angles. Here we go:
 |
| Question 1 |
 | ||
| Question 2 |
 |
| Question 3 |
 |
| Question 4 |
 |
| Question 5 |
 |
| Question 6 |
 |
| Question 7 |
I'm not gonna lie--I'm glad to get that achievement. But only two of those were even remotely challenging: questions 5 and 7 (the others had the angle measurements in the drawings). Still, I am delighted to report that by keeping my new rule in mind, I was able to identify those angles correctly!
And bonus: I have a trick to help my students who struggle with how to measure angles. Now, I don't know why this rule works . . . but it's good to have a little mystery in our lives:
 |
| There is more to know. . . . |
Thanks for stopping by!










